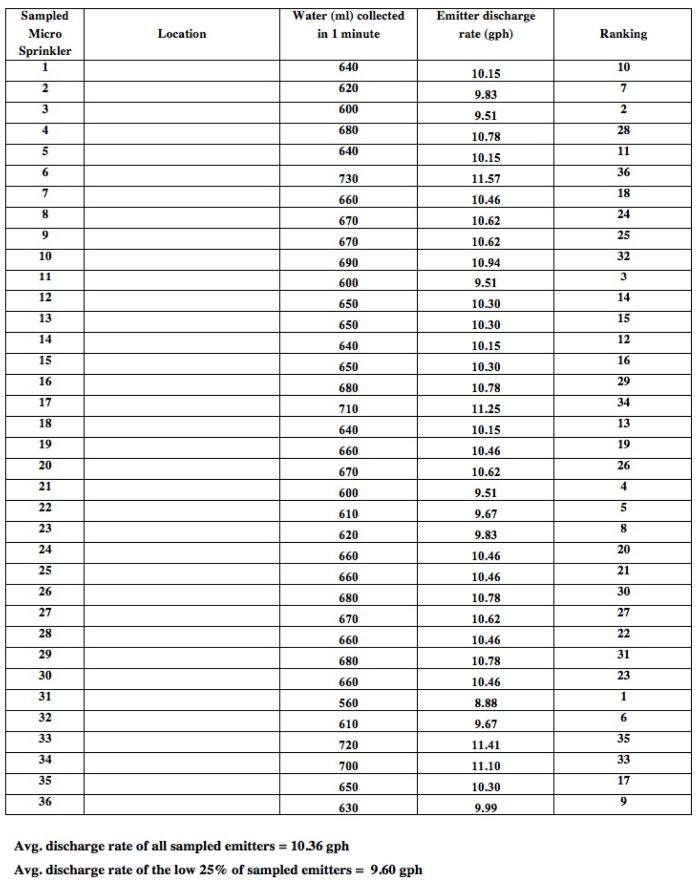
Microsprinkler evaluation example
Determining the average discharge rate

To determine the average discharge rate, add up all of the sampled microsprinkler discharge rates (column 4 of the table) and divide the sum by the number of sampled microsprinklers (36 in this case). Using the data from the table, the combined discharge rate values in column 4 divided by 36 (number of microsprinklers sampled) gives an average discharge rate of 10.4 gph.
Determining the average application rate
The microsprinkler discharge rate information from the system evaluation, while valuable, must be converted to an application rate before it can be used for irrigation scheduling (i.e., when and how much to irrigate).
In the example we’ve been using, there is only one microsprinkler per tree (tree spacing 16 ft. x 22 ft.) so the average application rate is the same as the microsprinkler’s average discharge rate (10.4 gph). The average application rate is therefore 10.4 gph per tree.
Irrigation scheduling and plant water use
Plant water use information is most commonly provided in terms of inches of water use per day (or per week or per month). Inches of water use is a difficult unit of measure to use with microirrigation systems, though, where the application rate is measured in gallons per hour.
To convert the per-tree water use from inches to gallons, use the following formula:
| Water use (gal/day) | = | Crop spacing (sq ft) | x | Water use (in/day) | x | 0.623 |
If the water use were expressed in terms of inches per week, the formula above could still be used but the result would be a water use in gallons per week. The same pattern would hold for any other time period.
Once the water use is in units of gallons per tree per time period, you can use the average application rate to determine how many hours you will need to operate the irrigation system. In our specific example, we could determine how many hours of irrigation, at a rate of 10.4 gph per tree, would be required to replace the calculated tree water use (gallons per tree per time period).
For example, if the almond orchard's water use were 0.25 in per day, the daily tree water use (determined using the above formula) would be:
| (16 x 22) sq ft | x | 0.25 in/day | x | 0.623 | = | 55 gal/day |
5.3 hours of irrigation time (55 gallons ÷ 10.4 gal/hr = 5.3 hours) would be required per day to replace the 55 gallons of water use by the tree. Some additional hours of irrigation beyond the 5.3 hours would be needed to compensate for irrigation inefficiencies. If you do not know your system's actual efficiency, adding an additional 10 to 15% to the irrigation time would be a good place to start for a well-designed microsprinkler system. With microsprinklers, it is generally recommended that irrigations not be daily, but rather every 3 to 4 days between irrigations during peak water use periods.
Determining the distribution uniformity (DU)
The distribution uniformity is defined as:
| Distribution uniformity DU (%) |
= | Average of low quarter microsprinkler discharge rates | ÷ | Average of all microsprinkler discharge rates | x | 100 |
To determine the average of the low-quarter microsprinkler discharge rates, start by ranking all of the measured microsprinkler discharge rates, from lowest to highest, and averaging the lowest 25% of the discharge rates. For example, if 40 microsprinklers were measured, you would rank them lowest to highest, and then average the discharges of the 10 microsprinklers with the lowest discharge rates.
To determine an DU from the data shown in the following table requires that you also determine (1) the average of all the microsprinkler discharges measured (this was already determined as 10.4 gph), and (2) the average of the low-quarter discharge rate (in this case there are 36 sampled microspirnklers, so you determine the average of the 9 lowest discharge rate values).
You could rank the measured microsprinkler discharge rates by hand, from lowest to highest, but this would take a long time time. If you are familiar with a spreadsheet program, such as MicroSoft Excel however, the spreadsheet can handle all of the calculations and ranking easily, even for a large data sets.
The average of the low-quarter microsprinkler discharge rates for the data in the table is 9.6 gph. The average discharge rate of all the sampled emitters was 10.4 gph, so the distribution uniformity is 93% (9.6 gph ÷ 10.4 gph x 100). This is a very good distribution uniformity so the microsprinkler system would be considered to be very uniform.
Microsprinkler evaluation form